Learn, how to write tuning logics for Mutabor 3 and above. Mutabor is a software that allows to retune your MIDI equipment in realtime to any tuning you like, including mutable tunings.
Simple GUI setup
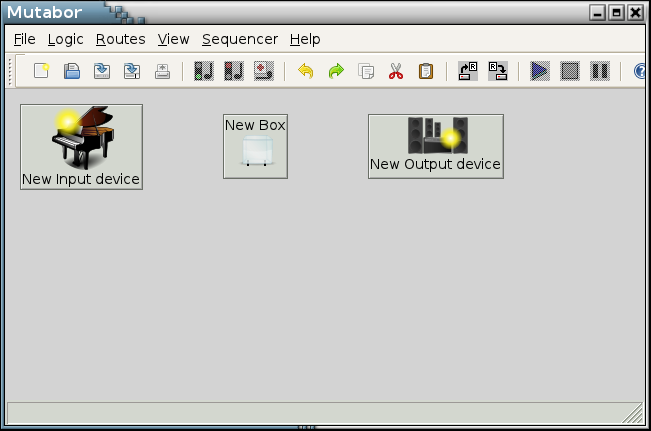
Now start Mutabor. It should greet you with the route editor window. If you didn't use Mutabor so far it will be empty except three buttons named “New input device”, “New Box” and “New output device”. A double click on “New input device” will open a dialog.
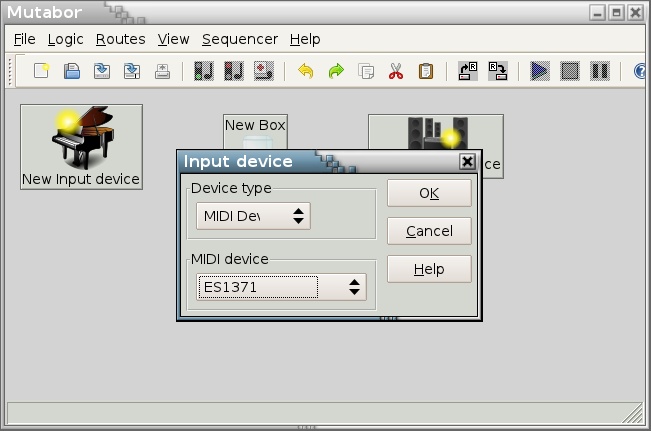
Choose the device, where your keyboard is connected to and click ok. With a double click on “New output device” you can select the output device.
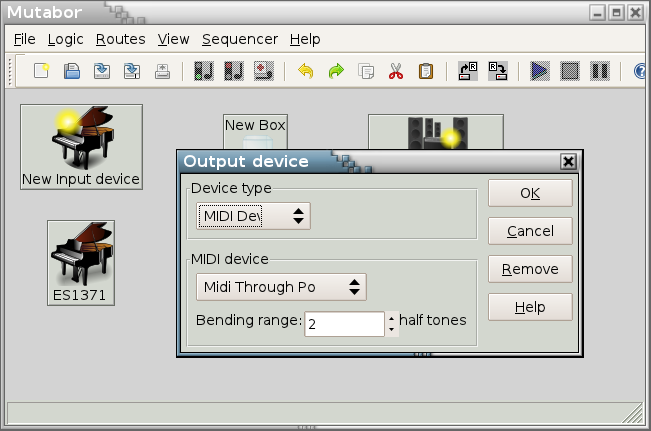
For MIDI files and devices you have to input the pitch bend range according to the settings of your device. Most devices initially have selected 2 semitones. Click on “OK”.
After selecting the devices double click on “New Box”. A new dialog will appear, that allows you to wire the input devices, the logic and the output devices according to your needs.
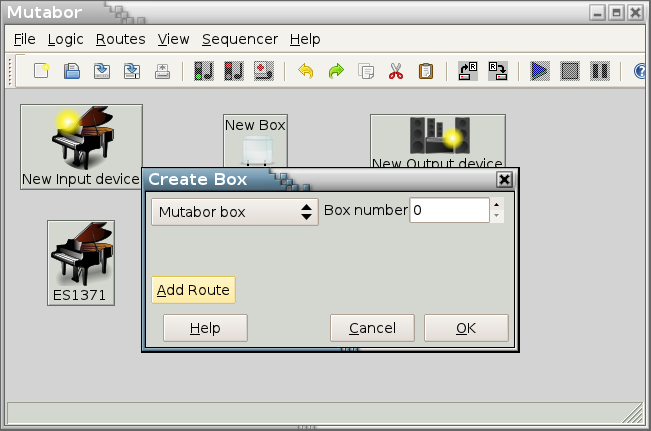
Click on “Add route”. A new row will of controls will appear. On the left hand side select your input device. The filter setting should remain at “all”. On the right hand side select your output device and select “all” for the filter settings.
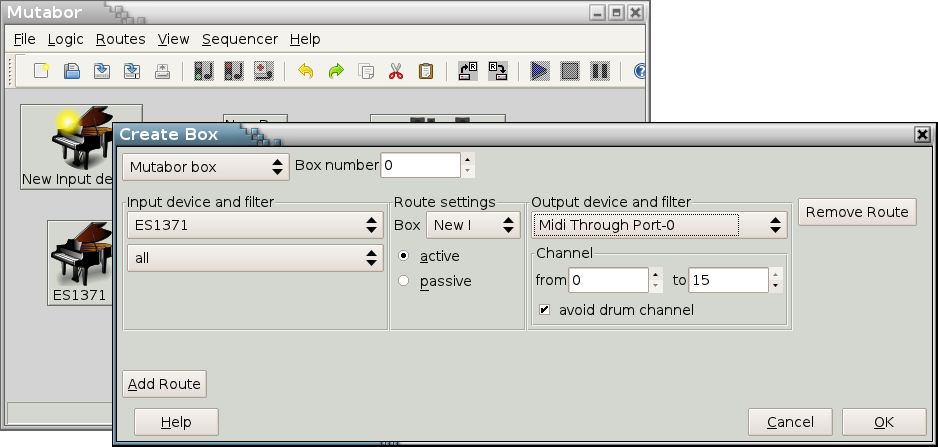
On top select “Mutabor box”, leave the box number unchanged and click “Ok”.
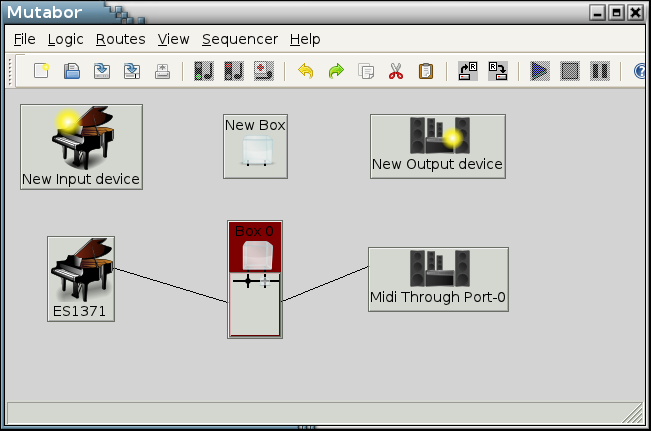
Via File->Open you can open the file “minimal.mut” and click on the green traffic light, in order to start it.
Now several windows appear and when you press any key on your MIDI keyboard, there should be some sound. Congratulations you set up Mutabor correctly.
A simple tuning logic
LOGIC definitions The definitions are separated by spaces. Each of these definitions has the form
name KEY character = initial_tuning [ commands ]The parameters are the following:
name - An arbitrary name, which consists of letters, numbers and the signs “'” and “_”
character - The key that has to be pressed on the computer keyboard in order to activate the logic
initial_tuning - The initial tuning that will be loaded, when this logic is activated
commands - A list of triggers and actions that describe the behaviour of the logic, we leave it empty for now
The simplest tuning is an equal tempered tuning. Lets assume we want a 12 tone equal temperament (12tet). So, we call the logic “equal” and want to activate it using the letter “e”. The tuning will be 12tet. Since names must not start with a digit, we will use the name “equal tempered 12 tone”, in short “et12t”. So the logic definition looks likeLOGIC
equal KEY e = et12t []
Trying to compile this tone system produces an error message. We have to define the tone system “et12t” first. A tone system is defined according toTONESYSTEM
The definitions are seperated by spaces. Each of them has the form
The parameters are defined as the following:
name - An arbitrary name, which consists of letters, numbers and the signs “'” and “_”
anchor key - a number between 0 and 127, which defines the MIDI code of the lowest piano key of the so called fundamental scale, the middle C has number 60 and the corresponding tone the number 69
fundamental scale - a comma separated list of tone names
repetition interval - the repetition interval is a name or interval expression, which will be used for repetition of the fundamental scale
As you can see, one important thing is the fundamental scale. It is a list of tones, which will be repeated throughout the whole MIDI pitch space, which spans integers from 0 to 127. Each repetition will be transposed with respect to its predecessor by the repetition interval. An empty tone denotes a silent key.
We choose the tone A' for the anchor key, which is usually tied to key 69. You can play with this number if you want to transpose your piece of music. Since we choose to define an equal tuning, we need only this single tone and the repetition interval, which is a half tone.
So our tuning logic looks like:LOGIC
equal KEY e = et12t []
TONESYSTEM
et12t = 69 [ A' ] half_tone
This logic is still not complete. We have to define the tone A' and must tell Mutaber what is meant by half_tone. Lets start with the tone A'. The easiest way to define it, is to assign a frequency to it. The syntax is as simple:TONE
where
Here the parameters are defined as:
name - An arbitrary name, which consists of letters, numbers and the signs “'” and “_”
frequency - a number that corresponds to the frequency in Hertz
Later we will use other description for tones.
We assign the tone A' to its usual frequency of 440 Hz and get the following logic:LOGIC
equal KEY e = et12t []
TONESYSTEM
et12t = 69 [ A' ] half_tone
TONE
A' = 440
At last we have to define the repetiton interval. The syntax for intervals is as simple:INTERVAL
where
Each interval must be defined according to the syntax:
Here the parameters are defined as:
name - An arbitrary name, which consists of letters, numbers and the signs “'” and “_”
interval expression - a description of the interval
There are several intuitive descriptions of intervals possible. We will use the syntax:
Using this we get the following logic:LOGIC
equal KEY e = et12t []
TONESYSTEM
et12t = 69 [ A' ] half_tone
TONE
A' = 440
INTERVAL
half_tone = 12 ROOT 2
Congratulations. You have written your first non-trivial tuning logic. Start the logic now, and you should get a window that allows you to click on exactly one icon.

Click on that icon to activate the tuning:
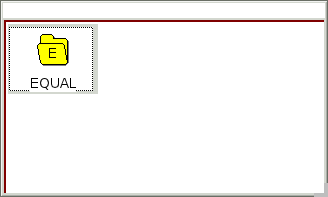
Now you can play some notes on your keyboard.
Small changes and improvements
An alternative half tone
half_tone2 = 1/12 octave
octave = 2:1
The second line follows the pattern
Having that in mind we can define a second tonesystem et12t2 by adding the code:TONESYSTEM
et12t2 = 69 [ A' ] half_tone2
INTERVAL
half_tone2 = 1/12 octave
octave = 2:1
But we don't want to replace the logic without checking that it is correct. So we must compare the two tunings. One easy way is to define two keyboard events for our logic. Remember, we hat defined the logic according to LOGIC Here each letter event calls a fixed tuning. The syntax of one trigger is
equal KEY e = et12t [
KEY m -> et12t
KEY i -> et12t2
]KEY were
LOGIC
equal KEY e = et12t [
KEY m -> et12t
KEY i -> et12t2
]
TONESYSTEM
et12t = 69 [ A' ] half_tone
TONE
A' = 440
INTERVAL
half_tone = 12 ROOT 2
TONESYSTEM
et12t2 = 69 [ A' ] half_tone2
INTERVAL
half_tone2 = 1/12 octave
octave = 2:1
As you can see, we can have each section multiple times in the logic program. This is helpful when we want to have all realated definitions as close as possible in the tuning logic.
Now you can load and start your logic with the semaphore button as described above. When you select a MIDI program (instrument) that produces stable tones like an organ, you will easily be able to compare the tunings.
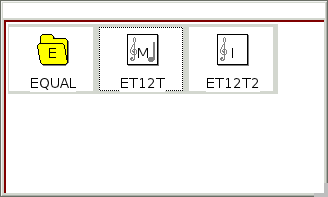
As you can see there are two additional icons, now. These are the computer keyboard events of your logic. They can be selected either by pressing the denoted key or by clicking on it. Select one by clicking on it, press a key and hold it down while you click the other tuning. You can see that the note on the icon will follow your click. It shows the active tuning. If you hear changing anything, then the two tunings differ. You can try to find out how much you can recognize by playing with the numbers in your logic. Change for example the ratio 1/12 into 12/143. You will be surprised, how easy it is to hear the changes.
The circle of fifth
LOGIC
equal KEY e = et12t [
KEY m -> et12t
KEY i -> et12t2
]
TONESYSTEM
et12t = 69 [ A' ] half_tone
TONE
A' = 440
INTERVAL
half_tone = 12 ROOT 2
TONESYSTEM
et12t2 = 69 [ A' ] half_tone2
INTERVAL
half_tone2 = 1/12 octave
octave = 2:1
LOGIC
fifth KEY f = et12fifth [
KEY j -> justfifth
]
TONESYSTEM
et12fifth = 69 [ A' ] 7 half_tone
justfifth = 69 [ A' ] just_fifth
INTERVAL
just_fifth = 3:2
As you can see we have added a new logic with a KEY event. The logic tunes to 12tet fifth and when you press the letter “j”, it retunes to the system of just fifth which are nearly perfectly tuned to our usual instruments: strings, winds, brass. Again you can compare the two tunings.
In order to make a tone system or pitch space from these tones, firstly, we must map them into one octave. This means, we have to define further tones:
TONE
E' = A' + just_fifth - octave
B' = E' + just_fifth
Fis' = B' + just_fifth - octave
Cis' = Fis' + just_fifth - octave
Gis' = Cis' + just_fifth
D' = A' - just_fifth
G' = D' - just_fifth + octave
C' = G' - just_fifth
F' = C' - just_fifth + octave
Bes' = F' - just_fifth + octave
Es' = Bes' - just_fifth
As' = Es' - just_fifth + octave
" ... "
The quotes “"” at the bottom delimit a comment. As you can see, we had to correct the pitch seven times by one octave. We usually replace As' by Gis' when we talk about music. In fact, there is a distance of one 5th of a half tone between them. So this enharmonic replacement would violate our rules. In order to be able to start the circle of fifth at any position, we choose the repetition interval such that all fifth are tuned just:
TONESYSTEM
circleoffifth = 63 [ Es', Bes', F', C',G',D',A',E',B',Fis',Cis',Gis' ] 12 just_fifth - 7 octave
When we want to play using one of the oldest such tuning systems, the Pythagorean tuning, we must rearrange the tones and will repeat this system shifted by an octave:
TONESYSTEM
pythagoras = 60 [ C', Cis', D', Es',E',F',Fis',G',Gis',A',Bes',B' ] octave
Let's add them to our tuning logic:LOGIC
equal KEY e = et12t [
KEY m -> et12t
KEY i -> et12t2
]
"12 tone equal temperament (12tet)"
TONESYSTEM
et12t = 69 [ A' ] half_tone
TONE
A' = 440
INTERVAL
half_tone = 12 ROOT 2
"12 tone equal temperament (alternative definition)"
TONESYSTEM
et12t2 = 69 [ A' ] half_tone2
INTERVAL
half_tone2 = 1/12 octave
octave = 2:1
LOGIC
fifth KEY f = et12fifth [
KEY j -> justfifth
KEY c -> circleoffifth
KEY p -> pythagoras
]
"12tet and just fifth"
TONESYSTEM
et12fifth = 69 [ A' ] 7 half_tone
justfifth = 69 [ A' ] just_fifth
INTERVAL
just_fifth = 3:2
TONE
E' = A' + just_fifth - octave
B' = E' + just_fifth
Fis' = B' + just_fifth - octave
Cis' = Fis' + just_fifth - octave
Gis' = Cis' + just_fifth
D' = A' - just_fifth
G' = D' - just_fifth + octave
C' = G' - just_fifth
F' = C' - just_fifth + octave
Bes' = F' - just_fifth + octave
Es' = Bes' - just_fifth
As' = Es' - just_fifth + octave
" ... "
"spiral of fifth an Pythagorean tuning"
TONESYSTEM
circleoffifth = 63 [ Es', Bes', F', C',G',D',A',E',B',Fis',Cis',Gis' ] 12 just_fifth - 7 octave
pythagoras = 60 [ C', Cis', D', Es',E',F',Fis',G',Gis',A',Bes',B' ] octave
Try to play all fifth in the tone system named “pythagoras”. You will one fifth that is very ugly.
A mutable tuning
We will fix one of the drawbacks of the pythagorean tuning: The bad fifth. For that we must define some rules which tell Mutabor, how to react on which events. Mutabor can recognize keys, harmonies, harmonic forms (all shifted versions of one pattern) and MIDI events. For now, it is sufficient to react on a harmonic form. As the Pythagorean tuning is based on a just fifth it would be nice, if each fifth could be just. This can be achieved, when we shift the interval structure to the actual active tones.
Lets start to explain it to Mutabor:PATTERN
fifth = {0, *3, *4, 7,*9}
This defines the pattern “fifth” as the combination of a reference key (0) and the fifth above it (7). Optionally, the keys 3, 4 and 9 can be pressed, as denoted by the asterisk “*”.
The retuning will be defined byRETUNING
transpo (distance) = @+distance []
This defines a retuning named “transpo”, which takes one parameter named “distance”. The name “distance” is one of the two parameters that have a special meaning. It tells the retuning the distance between the anchor key of the pattern (denoted by number 0) and the anchor key of the fundamental scale. The right hand site denotes the action. In this case it is a change of the anchor key of the tuning. The at sign “@” denotes the current anchor and the expression tells how to change it. Here, we move it to the anchor key of our pattern. This instructs Mutabor to move the fundamental scale from the old anchor key to a new one, transposing it so that from the old anchor tone the old pitch of the new anchor tone. So the latter one is never changed, while all the other tones might get assigned to a new frequency.
There are several different possibilities for defining such retunings. For further information we refer to the reference manual.
To finish our tuning, we must define a logic:
LOGIC
adaptive KEY a = pythagoras [
SHIFTED fifth -> transpo(distance)
]
The keyword “SHIFTED” denotes that the pattern is recognized in any transposition and that the parameter “distance” is set according to this transposition.
Finally, we can put everything together and get the following tuning logic:TONESYSTEM
pythagoras = 60 [ C', Cis', D', Es',E',F',Fis',G',Gis',A',Bes',B' ] octave
Let's add them to our tuning logic:LOGIC
equal KEY e = et12t [
KEY m -> et12t
KEY i -> et12t2
]
"12 tone equal temperament (12tet)"
TONESYSTEM
et12t = 69 [ A' ] half_tone
TONE
A' = 440
INTERVAL
half_tone = 12 ROOT 2
"12 tone equal temperament (alternative definition)"
TONESYSTEM
et12t2 = 69 [ A' ] half_tone2
INTERVAL
half_tone2 = 1/12 octave
octave = 2:1
LOGIC
fifth KEY f = et12fifth [
KEY j -> justfifth
KEY c -> circleoffifth
KEY p -> pythagoras
]
"12tet and just fifth"
TONESYSTEM
et12fifth = 69 [ A' ] 7 half_tone
justfifth = 69 [ A' ] just_fifth
INTERVAL
just_fifth = 3:2
TONE
E' = A' + just_fifth - octave
B' = E' + just_fifth
Fis' = B' + just_fifth - octave
Cis' = Fis' + just_fifth - octave
Gis' = Cis' + just_fifth
D' = A' - just_fifth
G' = D' - just_fifth + octave
C' = G' - just_fifth
F' = C' - just_fifth + octave
Bes' = F' - just_fifth + octave
Es' = Bes' - just_fifth
As' = Es' - just_fifth + octave
" ... "
"spiral of fifth an Pythagorean tuning"
TONESYSTEM
circleoffifth = 63 [ Es', Bes', F', C',G',D',A',E',B',Fis',Cis',Gis' ] 12 just_fifth - 7 octave
pythagoras = 60 [ C', Cis', D', Es',E',F',Fis',G',Gis',A',Bes',B' ] octave
"Mutable tuning: moving fifths."
PATTERN
fifth = {0, *3, *4, 7,*9}
RETUNING
transpo (distance) = @+distance []
LOGIC
adaptive KEY a = pythagoras [
SHIFTED fifth -> transpo(distance)
]
Closing
Mutabor has far more capabilities. It is possible to write even some tunings with Mutabor.